高速加法器

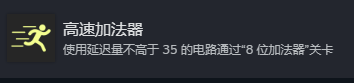
我们首先看常规的8位加法器

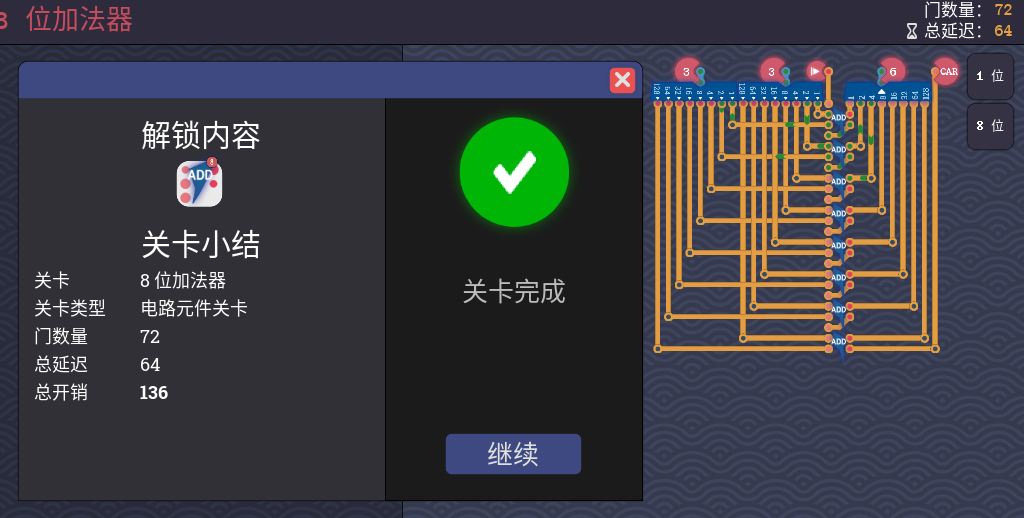
完全不行，离35差远了

打开延迟显示观察，可以发现主要问题在于每一个进位都依赖于前一个进位

8个进位叠加，延迟就大了

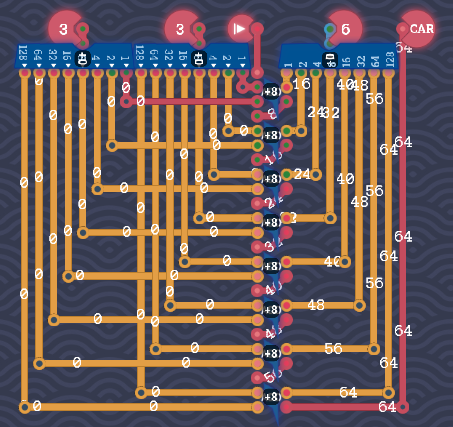
常规思路

此时很自然的思路是，能不能把全加器拆开，把进位优先处理，省下一些空间

每一个进位的含义是，这一路的 3 个输入是否有任意两个同时为 1

设两个输入分别是$A_0$_{$A_7$和$B_0$}$B_7$，每一个进位是$C_0$~$C_8$

记$A$ and $B$为 $AB$， $A$ or $B$ 为 $A+B$

那么$C_{i+1}=A_iB_i+A_iC_i+B_iC_i$

三路并联可以用开关减少延迟，三个且也可以用开关省空间，xor可以先留着

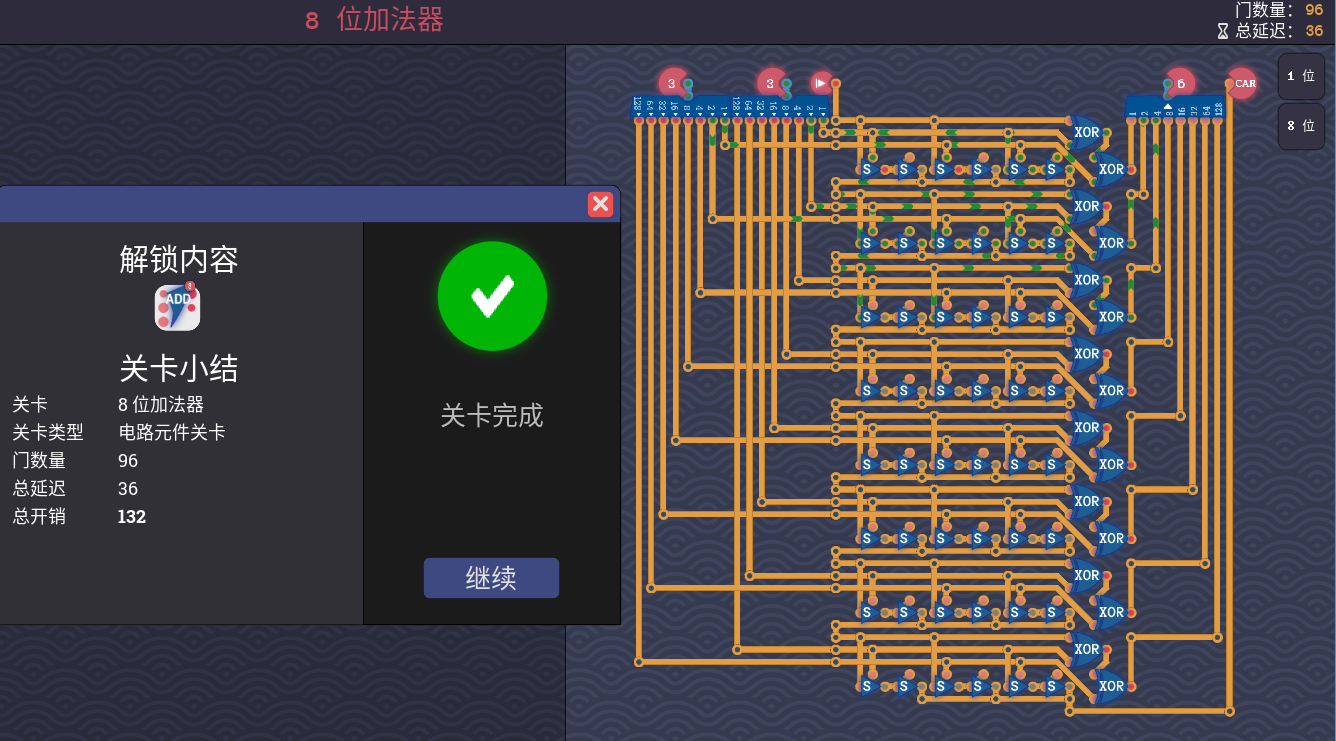
于是我们可以看到为什么成就要把标准设为35（x）

这里延迟的主要问题在于最后的两个 xor 导致了额外的 8 延迟

当然我们可以继续省 xor ，这里 xor 的含义是 3 路输入中有 1 个 1 或者 3 个 1

抽出一个 1 ，那么剩下的就是 2 个 1 (AND) 或者 2 个 0 (NOR)

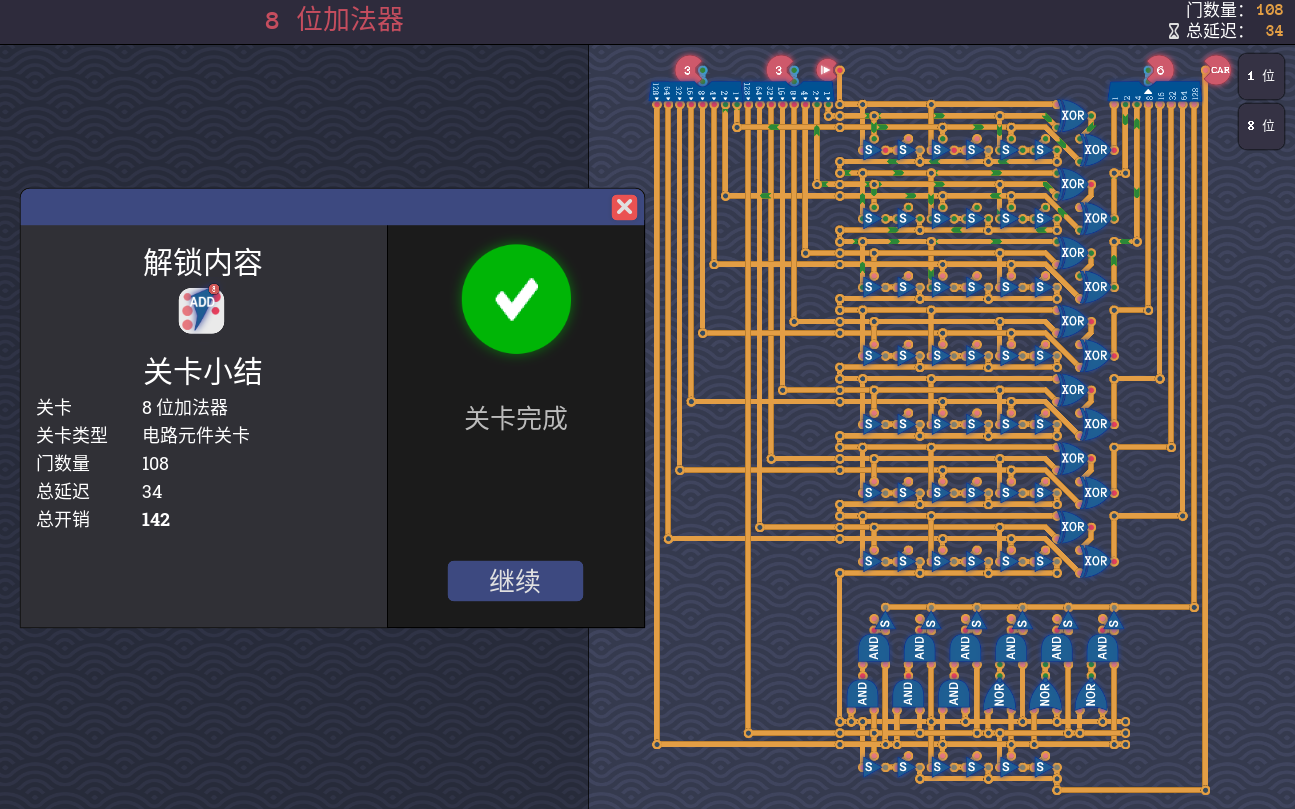
擦线拿到成就

其实还能再凹一点，让开关同时当 and 和 or ，这算是一个斜门过法（造出了4延时的全加器）

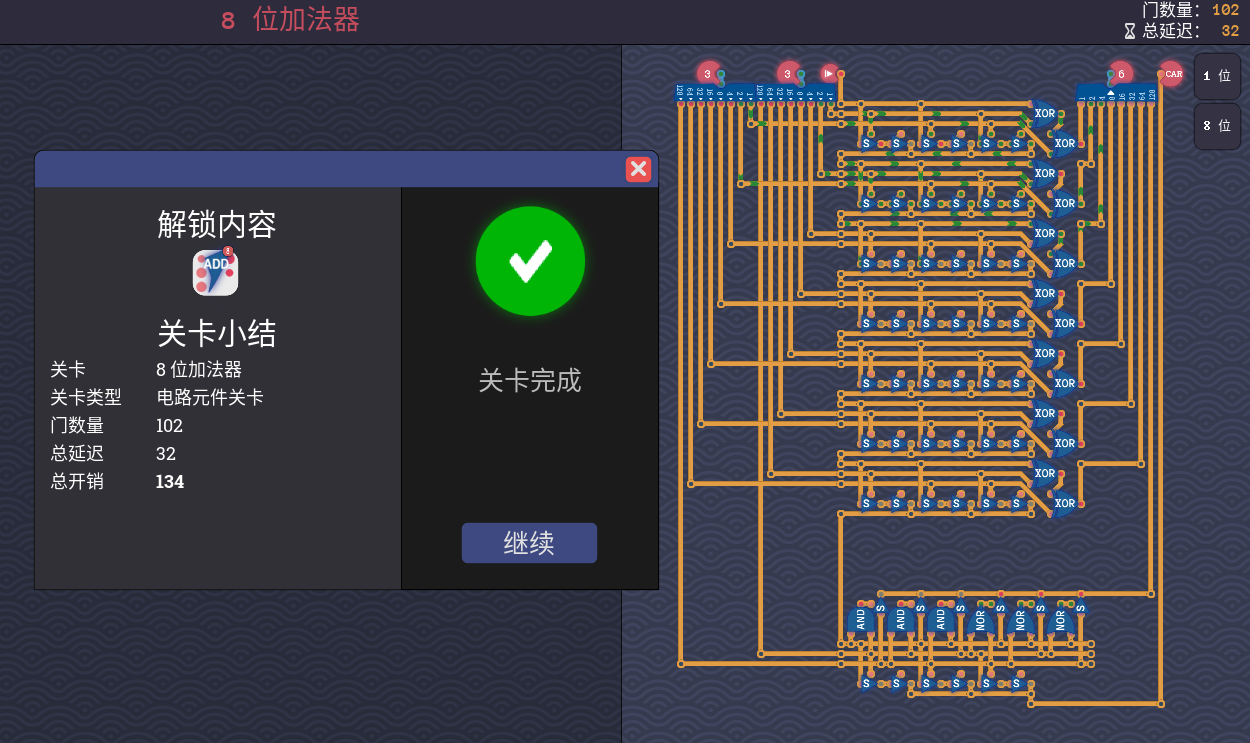
并行进位

之所以会高延迟，就是因为每一位的结果和进位都递归依赖于前一位的进位，那么只需要能够独立计算出每一位的结果和进位，就能够减少延迟了

xor 可以表示不进位的加法，那我们可以用 xor 先得到中间结果，单独计算每一位是否进位，然后再 xor 合并回来，得到最终结果

那么问题就变成了计算每一位的进位（而不是结果）

很显然，每一位的进位依旧依赖于之前所有位

当上一位上两个都是 1 （AND）时，必定进位（生成）

如果不是必定不进位（NOR），那么上上位进位时就必定进位（OR，传播），就需要考虑上上位，，直到碰到必定进位（AND）

每一位都必须考虑 AND 和 OR 以覆盖所有情况

所以第 n 位是否进位，条件是

上一位是 AND

或者 上一位是 OR 且 上上位是 AND

或者 上一位是 OR 且 上上位是 OR 且 上上上位是 AND

或者 上一位是 OR 且 上上位是 OR 且 上上上位是 OR 且 上上上上位是 AND

...

或者 上一位是 OR 且 .... 且 初始进位

$C_{i+1}=A_iB_i+A_iC_i+B_iC_i=A_iB_i+(A_i+B_i)C_i$

设生成信号$G_i=A_iB_i$，传播信号$P_i=A_i+B_i$

那么

$$C_{i+1}=G_i+P_iC_i$$

$$=G_i+P_i(G_{i-1}+P_{i-1}C_{i-1})$$

$$=G_i+P_iG_{i-1}+P_iP_{i-1}C_{i-1}$$

$$=G_i+P_iG_{i-1}+P_iP_{i-1}(G_{i-2}+P_{i-2}C_{i-2})$$

$$=G_i+P_iG_{i-1}+P_iP_{i-1}G_{i-2}+P_iP_{i-1}P_{i-2}C_{i-2}$$

$$...$$

$$=G_i+P_iG_{i-1}+...+P_i...P_0C_0$$

即

$$C_{i+1}=G_i+P_iG_{i-1}+...+P_i...P_0C_0$$

这里的或可以用开关并联来省延迟，这里的且可以用二分法来省延迟

为了重复利用已有的结果，需要一定的规划

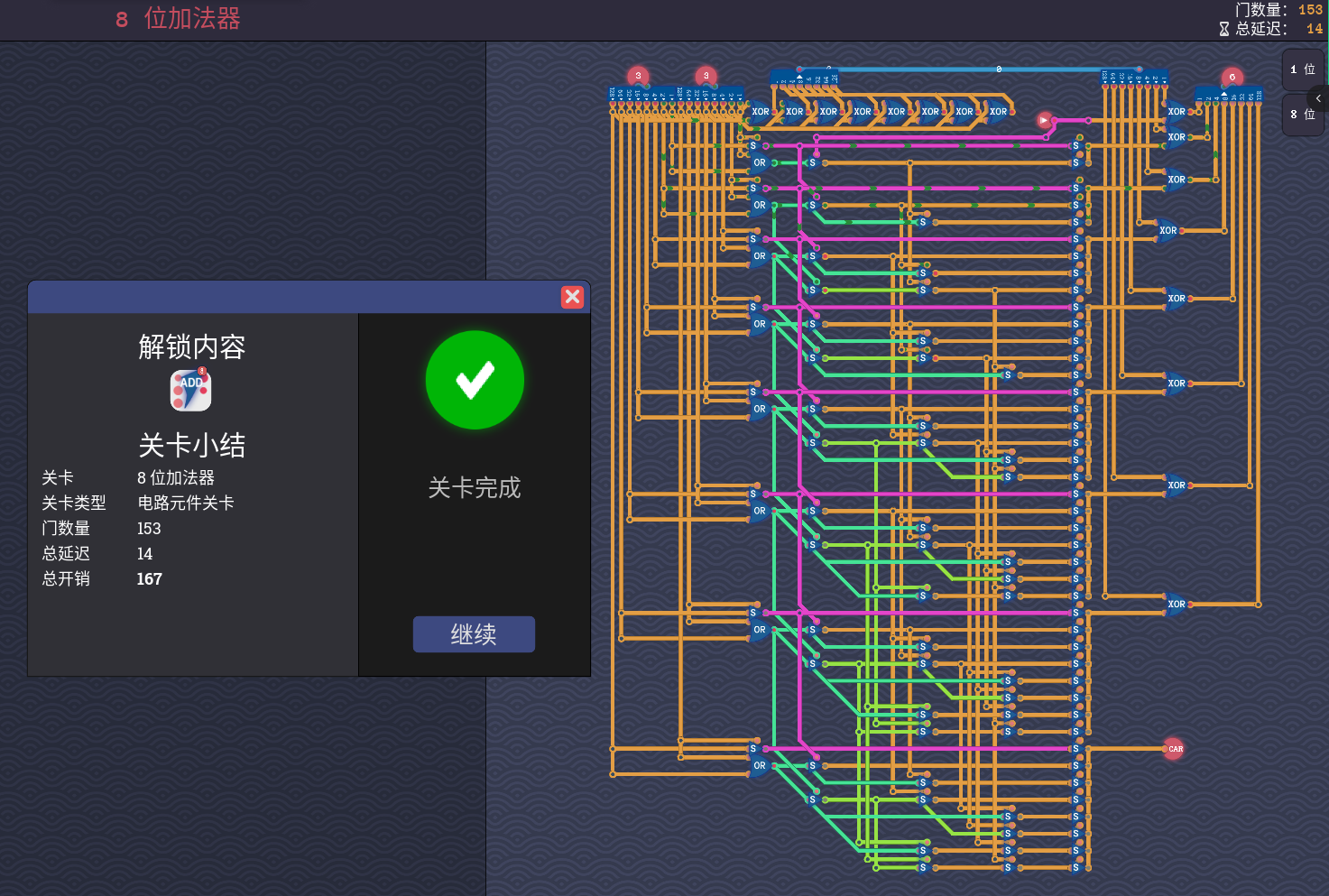
摆出来就是 14 延迟

其实且和或是可以相互转换的，两边加上 NOT 就能再用开关的并联继续省延迟

可以把 AND 和 OR 换成 NAND 和 NOR 继续省

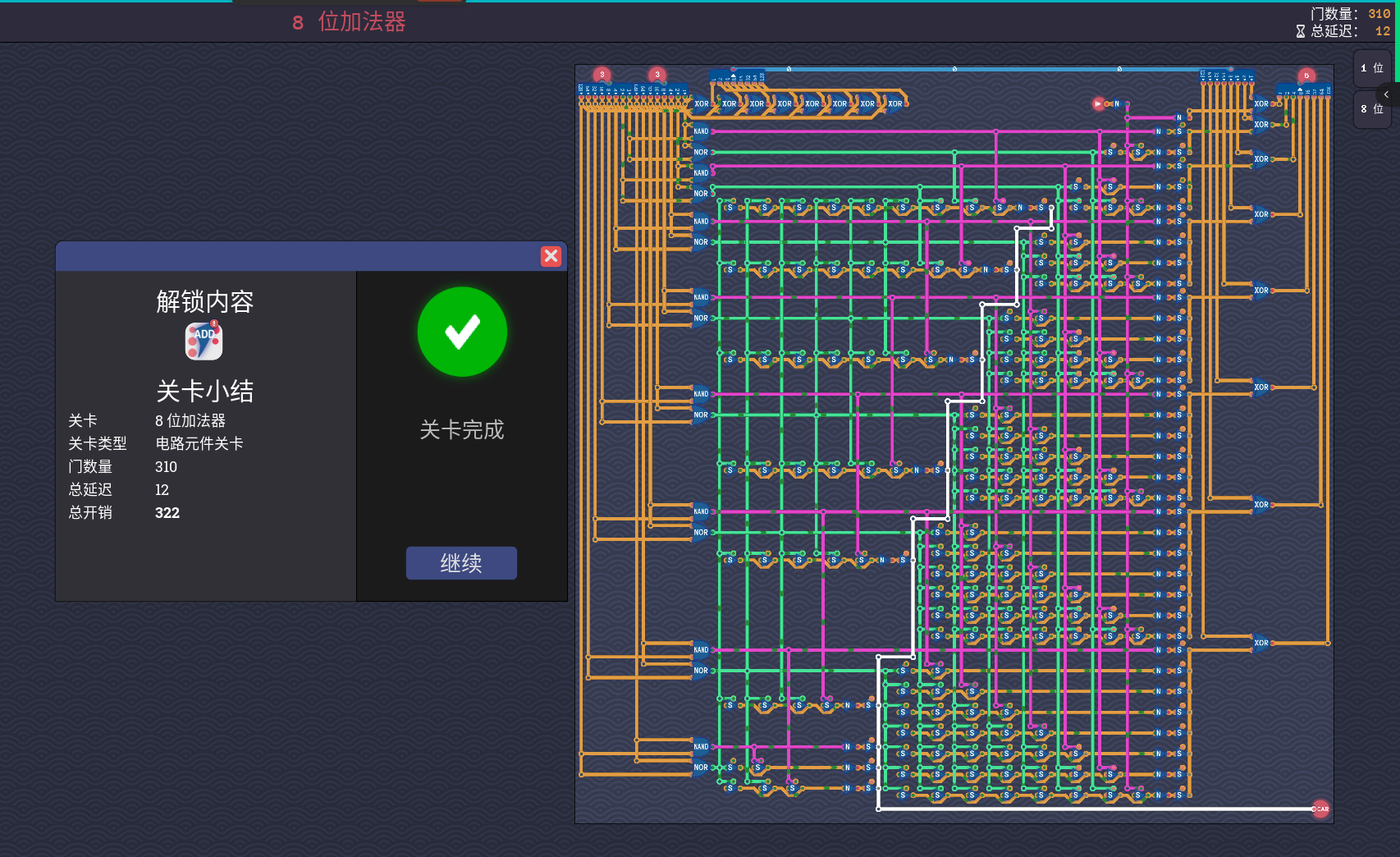
达到 12 延迟

中间我感觉有许多重复的模式，不过不知道有没有办法省下来，就硬穷举了