2.2 流体运动方程

流体动力学基于这样一个假设：流动的长度尺度总是被认为大于构成粒子的平均自由程，因此流体可以被视为连续体。这个模型使得可以在空间中的一点处理流体性质（如速度、压力、密度等），物理变量是空间和时间的连续函数。换句话说，我们假设我们系统的宏观行为与物质分布完全连续的情况相同。因此，当我们谈论"质量元素"（或"流体粒子"）的速度时，我们总是指包含在有限范围的小体积内的大量构成粒子的平均速度，尽管这个体积必须被视为一个点。

从连续体角度对流体运动的数学描述允许两种不同的方法。第一种称为拉格朗日描述,它识别每个质量元素并描述它随时间的变化。从数学上讲,我们用函数表示运动:

$$\mathbf{r} = \mathbf{r}(\mathbf{R}, t),\tag{2.1}$$

相关信息

r : (r0: Pos, t: Time) -> Pos

其中$\mathbf{R} = (X_1, X_2, X_3)$是流体粒子在$t = 0$时（假设）的原始位置,而$\mathbf{r} = (x_1, x_2, x_3)$是同一质量元素在随后时刻$t$的位置。因变向量$\mathbf{r}$由此被确定为独立变量$\mathbf{R}$和$t$的函数。流体粒子的速度和加速度是

$$\mathbf{v}(\mathbf{R}, t) = \frac{\partial\mathbf{r}}{\partial t} \quad \text{和} \quad \mathbf{a}(\mathbf{R}, t) = \frac{\partial^2\mathbf{r}}{\partial t^2},\tag{2.2}$$

其中偏导数表示对给定质量元素（即,保持$\mathbf{R}$不变）进行微分。

相关信息

v : (r0: Pos, t: Time) -> Vel
v = ∂r / ∂t
a : (r0: Pos, t: Time) -> Acc
a = ∂∂r / ∂t / ∂t

第二种方法,称为欧拉描述,关注空间中的特定点,并描述该点随时间的流动。从数学上讲,运动状态由速度场描述

$$\mathbf{v} = \mathbf{v}(\mathbf{r}, t),\tag{2.3}$$

其中独立变量是空间位置,由向量$\mathbf{r} = (x_1, x_2, x_3)$表示,以及时间。流体粒子的加速度是速度的物质导数。因此,我们有

$$\mathbf{a}(\mathbf{r}, t) = \frac{D\mathbf{v}}{Dt} = \frac{\partial\mathbf{v}}{\partial t} + (\mathbf{v} \cdot \text{grad})\mathbf{v}.\tag{2.4}$$

同样,可以定义物质导数

$$\frac{DQ}{Dt} = \frac{\partial Q}{\partial t} + (\mathbf{v} \cdot \text{grad})Q,\tag{2.5}$$

它测量当我们沿流体粒子的路径移动时量$Q$的变化率。

梯度

grad : (Pos -> R) -> (Pos -> Vec)
grad f = ((∂f / ∂e) for e in Pos.base)

梯度接收一个标量场返回一个向量场

它只是对每个基的方向求个偏导，然后装在一起，就是散装导数

对于每个基的方向

• 基的方向/值增加的方向/向量正方向 是重合的
• 偏导大小正比值增加的程度
• 无穷小的范围，（我们所考虑的）场是线性的

所以合并起来能表示增加最快的方向

物质导数

v : (r: Pos, t: Time) -> Vel
a : (r: Pos, t: Time) -> Acc
a = Dv / Dt
  = ∂v / ∂t + (v · grad) v
  = ∂v / ∂t + (v · grad v.x,
               v · grad v.y,
               v · grad v.z)

$v$ 关注空间中静止点 $r$ 某一刻 $t$ 的速度

当取确定的时刻 $t$ 时，$v$ 表示一个速度场

当我们关注固定点的速度变化时不需要物质导数，可以直接 $∂v/∂t$

但是关注粒子的加速度时，就需要考虑粒子在往某个方向移动，因为速度场的不均匀有额外的梯度变化率 $(v · grad)v$

$(v · grad)$ 是个算子，按照形式计算下来是一个“数”，能接收一个标量，或矢量（依次作用于每个分量），但是运算不是线性的

从右往左读，它会求出每个量的梯度（$grad$），然后与当前速度点乘，求出当前速度下这个量增大的程度(变化率)

2.2.1 守恒原理

我不打算推导流体动力学的基本方程,因为它们可以在许多教科书中找到。在本节中,我将列出这些方程,使用欧拉规范,在惯性参考系中。

在流体内部没有物质源或汇的情况下,质量守恒由连续性方程表示,

$$\frac{1}{\rho} \frac{D\rho}{Dt} + \text{div}\mathbf{v} = 0.\tag{2.6}$$

这个方程说明质量元素的密度变化率和体积变化率在大小上相等但符号相反。

散度

div : (Pos -> Vec) -> (Pos -> R)
div f = sum(∂f.e / ∂e for e in Pos.base)

散度接收一个向量场返回一个标量场

可以粗略理解：

某一点的散度，是一个以 $(x,y,z)$ 和 $(x,y,z)+(dx,dy,dz)$ 为顶点的立方体，它表面向外通量的和，除以其体积

对于每个分量例如 $x$ ，其分量偏导的定义正好等于，立方体单位体积下相对两个面向外的通量之和 （因为反方向向外的通量正好需要加个负号），因此三个偏导加起来正好是单位体积向外的全部通量

$$(f_x(x+dx,y,z)-f_x(x,y,z))dydz=(\frac{∂f_x}{∂x}dx)dydz$$

接下来具体理解：

我们可以建立这样的数学直观：一维速度导数就是散度

或者说，当把函数作为速度场理解时，导数就是散度，其大小也就是函数倾斜程度表示了这一点向外发散或汇聚的程度

速度在一点增大的程度与这一点向外的力成正比，这很合理

向外的通量 $f(x+dx) - f(x)$ 除以体积 $dx$ 就是导数，也是散度

由于无穷小范围下，（我们所考虑的）场是线性的（一个真正意义上的点），我们可以舍弃一阶以下的项（这就是为什么微积分能起作用），分别考虑每个方向的效应，然后将它们叠加，这就是它的定义形式

$$\text{div} f = \frac{∂f_x}{∂x}+\frac{∂f_y}{∂y}+\frac{∂f_z}{∂z}$$

连续性方程

我想到了两种方式推出连续性方程

设体积微元 $dV$ 的质量是 $dm$，那么

$$0 =\frac{Ddm}{Dt} =\frac{D\rho dV}{Dt} =dV\frac{D\rho}{Dt}+\rho\frac{DdV}{Dt}$$

可以得到

$$\frac{D\rho}{\rho Dt}+\frac{DdV}{dVDt}=0$$

这表示了相对密度和相对体积的物质导数某种意义上是对称的——其中一个减少意味着另一个增大

并且注意到相对体积的物质导数，实际上就是单位体积向外的速度通量，也就是 $\text{div}\mathbf{v}$

于是得到连续性方程

$$\frac{D\rho}{\rho Dt}+\text{div}\mathbf{v}=0$$

另一种思路是从另一种形式出发

考虑静止的某一邻域，其密度增加的程度应该与其流出质量的程度相反

$$\frac{\partial\rho}{\partial t}+\text{div}(\rho\mathbf{v})=0$$

展开第二项（每一项的偏导都使用乘法展开），变成

$$\frac{\partial\rho}{\partial t}+\mathbf{v}·\text{grad}\rho+\rho\text{div}(\mathbf{v})=0$$

这里

• 第一项表示这一点密度增加的程度
• 第二项表示密度在速度方向受密度分布影响而增大的程度
  • 当密度均匀时此项为0
• 第三项表示密度不变的前提下体积变大的倾向
  • 当不可压缩时此项为0

注意到前两项之和就是物质导数的定义，于是有

$$\frac{D\rho}{D t}+\rho\text{div}(\mathbf{v})=0$$

两边除以 $\rho$ 就能得到原式

牛顿第二运动定律可以写成

$$\frac{D\mathbf{v}}{Dt} = \mathbf{g} - \frac{1}{\rho}\text{grad}p + \frac{1}{\rho}\mathbf{f}(\mathbf{v}),\tag{2.7}$$

方程解释

这里的单位是单位体积的加速度

• 第一项是体积力(重力造成的加速度)
• 第二项是压力梯度(由压力的不均衡分布造成的加速度，负号是因为压力从压力大的地方指向压力小的地方)
• 第三项是粘性应力(剪切和拉伸/压缩产生的加速度/耗散)

其中$\mathbf{g}$是重力加速度，$\rho$是密度，$p$是压力。向量$\mathbf{f}$是单位体积的粘性力，可以写成粘性应力张量$\tau$的矢量散度。对于牛顿流体，这个对称张量的六个分量是

$$\tau_{ij} = \mu \left(\frac{\partial v_i}{\partial x_j} + \frac{\partial v_j}{\partial x_i} - \frac{2}{3}\delta_{ij}\frac{\partial v_k}{\partial x_k}\right) + \mu_\vartheta\delta_{ij}\frac{\partial v_k}{\partial x_k},\tag{2.8}$$

其中剪切粘度$\mu$和体积粘度$\mu_\vartheta$系数都依赖于局部热力学性质（仅当$\delta_{ij} = 1$如果$i = j$，$\delta_{ij} = 0$如果$i \neq j$；求和是对重复指标进行的）。

爱因斯坦求和约定

这个表达式中出现了哑指标k，根据爱因斯坦求和约定，需要进行求和。具体来说：

$$\begin{aligned} \frac{\partial v_k}{\partial x_k} &= \frac{\partial v_1}{\partial x_1}+\frac{\partial v_2}{\partial x_2}+\frac{\partial v_3}{\partial x_3} \\ &= \frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z} \\ &=\text{div}\mathbf{v} \end{aligned}$$

（1,2,3分别表示x,y,z）

是体积变化率

如果表达式有多个哑变量，将整体进行加和，举例来说

$$\begin{aligned} \frac{\partial f}{\partial x_k}e_k&=\frac{\partial f}{\partial x_1}e_1+\frac{\partial f}{\partial x_2}e_2+\frac{\partial f}{\partial x_3}e_3 \\ &=\begin{bmatrix} \frac{\partial f}{\partial x}\\[0.5em] \frac{\partial f}{\partial y}\\[0.5em] \frac{\partial f}{\partial z} \end{bmatrix} \\ &=\text{grad}f \end{aligned}$$

克罗内克(Kronecker)δ函数

$$\delta_{mn} = \begin{cases} 1 & \text{if } m = n \\ 0 & \text{if } m \neq n \end{cases}$$

也就是对于 $i\neq j$ 有

$$\tau_{ij} = \mu \left(\frac{\partial v_i}{\partial x_j} + \frac{\partial v_j}{\partial x_i}\right)$$

对于 $i = j$ 有

$$\tau_{ij} = \mu \left(\frac{\partial v_i}{\partial x_i} + \frac{\partial v_i}{\partial x_i} - \frac{2}{3}\frac{\partial v_k}{\partial x_k}\right) + \mu_\vartheta\frac{\partial v_k}{\partial x_k}$$

张量

标量是 0 阶张量，矢量是 1 阶张量，粘性应力张量 $\mathbf{\tau}$ 是 2 阶张量

2 阶张量通常用 3x3 矩阵表示(在三维空间中)，每个元素代表应力在不同面和方向上的分量

$$\mathbf{\tau}=\begin{bmatrix} \tau_{xx} & \tau_{xy} & \tau_{xz} \\ \tau_{yx} & \tau_{yy} & \tau_{yz} \\ \tau_{zx} & \tau_{zy} & \tau_{zz} \end{bmatrix}$$

$\tau_{ij}$ 是标量，表示 $i$ 法平面上 $j$ 正方向的力的大小，例如 $\tau_{xx}$ 表示 $x$ 方向上向外的力（因为反方向必定大小相等方向相反）

每一行是一个法平面上的矢量力，每一列是每个方向在不同法平面上的力

对于体积微元，反面的应力大小相等方向相反(力的变化用其它方式表示)，因此只需要三个面

为了力矩平衡，有 $\tau_{ij}=\tau_{ji}$ (旋转通常用其它方式表示)，所以实际上独立的只有6个分量

其中对角线上的分量是正应力，作用在垂直于面的方向，三个加起来就是各向同性的作用力

其余分量是剪应力，作用在平行于面的方向

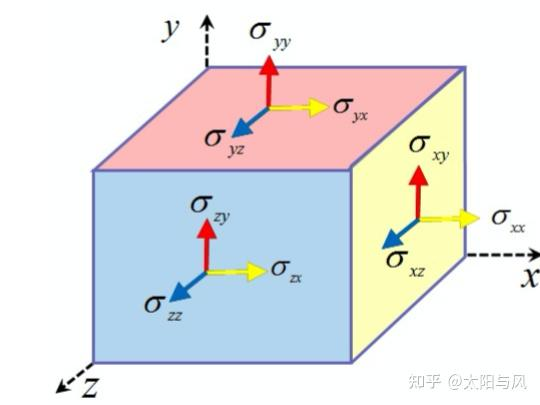应力张量

牛顿流体的应力张量是

$$\sigma_{ij} = -p\delta_{ij}+\tau_{ij}$$

含有 $\delta_{ij}$ 的项表示在张量对角线上，表示各向同性向外的力

其中 $-p\delta_{ij}$ 为静水压力，其中标量 $p$ 表示平均压力大小，加负号是因为需要保证 $p$ 为正时压力向内

粘性应力张量（也就是前面的式子）

$$\tau_{ij} = \mu \left(\frac{\partial v_i}{\partial x_j} + \frac{\partial v_j}{\partial x_i} - \frac{2}{3}\delta_{ij}\frac{\partial v_k}{\partial x_k}\right) + \mu_\vartheta\delta_{ij}\frac{\partial v_k}{\partial x_k}$$

第一项为体积不变时的应力，第二项为体积变化时的应力

先看第二项，含有 $\delta_{ij}$ ，表示拉伸作用

这里的和（张量的迹）正比于体积变化率（速度散度），表示这个应力与体积变化率成正比

它是体积变化时由粘性导致的阻力，不出意外 $\mu_\vartheta$ 应该是个负值

再看第一项，记为

$$s_{ij} = \mu \left(\frac{\partial v_i}{\partial x_j} + \frac{\partial v_j}{\partial x_i} - \frac{2}{3}\delta_{ij}\frac{\partial v_k}{\partial x_k}\right)$$

有

$$\sum_is_{ii} = 0 \tag{*}$$

接下来我们尝试推出 $s_{ij}$

矢量的梯度就是对矢量的每一个分量分别求梯度，也构成张量

速度梯度张量

$$L = \text{grad} \mathbf{v} = \begin{bmatrix} \frac{\partial v_x}{\partial x} & \frac{\partial v_x}{\partial y} & \frac{\partial v_x}{\partial z} \\ \frac{\partial v_y}{\partial x} & \frac{\partial v_y}{\partial y} & \frac{\partial v_y}{\partial z} \\ \frac{\partial v_z}{\partial x} & \frac{\partial v_z}{\partial y} & \frac{\partial v_z}{\partial z} \end{bmatrix}$$

$i\neq j$ 时的剪切应力就是速度梯度张量的对称部分乘以粘度系数

$$s'_{ij} = \mu \left(\frac{\partial v_i}{\partial x_j} + \frac{\partial v_j}{\partial x_i}\right)$$

$i=j$ 时不能直接设为 0 ，我们不需要体积变化，但是它形状会变化

我们在对角线上减去它的平均值保证体积不变 $(\text{tr}(\tau)=0)$

平均值是

$$\frac{1}{3}\sum_is'_{ij} = \frac{1}{3}\sum_i2\mu\frac{\partial v_i}{\partial x_i} = \frac{2}{3}\mu\frac{\partial v_k}{\partial x_k}$$

于是

$$\begin{aligned} s_{ij} &= \mu \left(\frac{\partial v_i}{\partial x_j} + \frac{\partial v_j}{\partial x_i}\right) - \frac{2}{3}\mu\frac{\partial v_k}{\partial x_k}\delta_{ij} \\ &= \mu \left(\frac{\partial v_i}{\partial x_j} + \frac{\partial v_j}{\partial x_i} - \frac{2}{3}\delta_{ij}\frac{\partial v_k}{\partial x_k}\right) \end{aligned}$$

额外信息

作为补充，牛顿流体的粘性应力张量与应变率张量关系密切

速度梯度张量可以分解为对称部分和反对称部分，它们相互正交

$$L = D+W = \frac{1}{2}\left(L+L^T\right) + \frac{1}{2}\left(L-L^T\right)$$

对称部分 $D$ 是应变率张量，描述了材料在某一时刻的变形速率，不考虑材料的旋转或刚体运动

$$D_{ij} = \frac{1}{2}\left(\frac{\partial v_i}{\partial x_j} + \frac{\partial v_j}{\partial x_i}\right)$$

反对称部分 $W$ 是自旋张量，描述了材料的旋转运动，而不是形变

$$W_{ij} = \frac{1}{2}\left(\frac{\partial v_i}{\partial x_j} - \frac{\partial v_j}{\partial x_i}\right)$$

考虑到体积不变的条件，可以定义偏应变率张量：

$$D'_{ij} = D_{ij} - \frac{1}{3}\delta_{ij}D_{kk}$$

其中 $D_{kk} = \frac{\partial v_k}{\partial x_k}$ 是应变率张量的迹，乘以 $\frac{1}{3}$ 取平均值

那么 $s_{ij}$ 可以简洁地写为：

$$s_{ij} = 2\mu D'_{ij}$$

张量的矢量散度

张量的矢量散度就是对张量矩阵的每一行(一个法平面上的矢量)求散度，得到 3 个标量构成矢量

体积微元由应力不均匀而受到的力由应力张量的矢量散度描述

$$\mathbf{f} = \frac{\partial \tau_{ij}}{\partial x_j}e_i$$

这里 $e_i$ 是基向量

我们展开看每个分量的组成

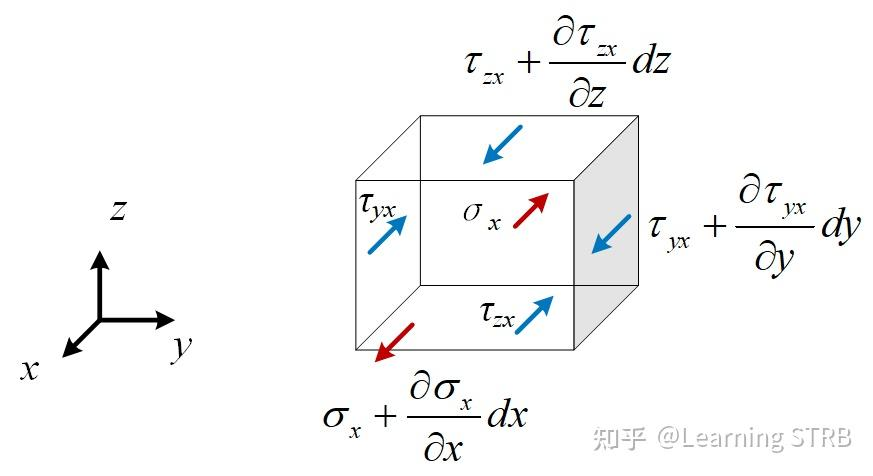平衡方程

$$\begin{aligned} f_i &= \frac{\partial \tau_{ix}}{\partial x} + \frac{\partial \tau_{iy}}{\partial y} + \frac{\partial \tau_{iz}}{\partial z} \\ &= \frac{\partial \tau_{xi}}{\partial x} + \frac{\partial \tau_{yi}}{\partial y} + \frac{\partial \tau_{zi}}{\partial z} \end{aligned}$$

每方向上的分力是对应法平面上应力的散度（单位体积内流出的通量，由于力矩的对称性，都变成了正方向的力）

我们将 $\tau_{ij}$ 代入 $f_i$ ：

$$\begin{aligned} f_i &= \frac{\partial \tau_{ij}}{\partial x_j} \\ &= \mu \frac{\partial}{\partial x_j}\left(\frac{\partial v_i}{\partial x_j} + \frac{\partial v_j}{\partial x_i}\right) - \frac{2}{3}\mu\delta_{ij}\frac{\partial}{\partial x_i}\left(\frac{\partial v_k}{\partial x_k}\right) + \mu_\vartheta\delta_{ij}\frac{\partial}{\partial x_i}\left(\frac{\partial v_k}{\partial x_k}\right) \\ &= \sum_j\mu \frac{\partial}{\partial x_j}\left(\frac{\partial v_i}{\partial x_j} + \frac{\partial v_j}{\partial x_i}\right) - \sum_k\frac{2}{3}\mu\frac{\partial}{\partial x_i}\left(\frac{\partial v_k}{\partial x_k}\right) + \sum_k\mu_\vartheta\frac{\partial}{\partial x_i}\left(\frac{\partial v_k}{\partial x_k}\right) \\ &= \sum_j\mu\frac{\partial}{\partial x_j}\frac{\partial}{\partial x_j}v_i + \sum_j\mu\frac{\partial}{\partial x_i}\left(\frac{\partial v_j}{\partial x_j}\right) - \frac{2}{3}\mu\frac{\partial}{\partial x_i}\text{div}\mathbf{v} + \mu_\vartheta\frac{\partial}{\partial x_i}\text{div}\mathbf{v} \\ &= \mu\nabla^2v_i + \mu\frac{\partial}{\partial x_i}\text{div}\mathbf{v} - \frac{2}{3}\mu\frac{\partial}{\partial x_i}\text{div}\mathbf{v} + \mu_\vartheta\frac{\partial}{\partial x_i}\text{div}\mathbf{v} \\ &= \mu\nabla^2v_i + \left(\frac{1}{3}\mu + \mu_\vartheta\right)\frac{\partial}{\partial x_i}\text{div}\mathbf{v} \end{aligned}$$

于是

$$\begin{aligned} \mathbf{f} &= f_ie_i \\ &= \mu\nabla^2v_ie_i + \left(\frac{1}{3}\mu + \mu_\vartheta\right)\frac{\partial \text{div}\mathbf{v}}{\partial x_i}e_i \\ &= \mu\nabla^2\mathbf{v} + \left(\frac{1}{3}\mu + \mu_\vartheta\right)\text{grad}(\text{div}\mathbf{v}) \end{aligned}$$

书上这里把系数搞反了

因此，我们有

$$\mathbf{f}(\mathbf{v}) = \mu\nabla^2\mathbf{v} + \left(\mu + \frac{1}{3}\mu_\vartheta\right)\text{grad}(\text{div}\mathbf{v}),\tag{2.9}$$

这里为了简单起见，我们假设粘度系数在运动场中保持恒定。方程(2.7)通常被称为纳维-斯托克斯方程(N-S方程)。

如果流动的压力变化不产生任何显著的密度变化，则可以忽略流体的可压缩性。（这在大多数液体流动中发生，也在气体流动中发生，其中速度处处远小于声速。）然而，在不可压缩流动中，总是需要用基于热力学原理的方程来增补方程(2.6)和(2.7)。具体来说，热能守恒意味着

人话

许多情况可以看作不可压缩流动。

在不可压缩流动中，密度变化可以忽略，但仍需要考虑热能守恒。

这是因为即使密度不变，温度和压力的变化仍可能影响流体的行为。

我们需要据此增补质量守恒

$$\frac{1}{\rho} \frac{D\rho}{Dt} + \text{div}\mathbf{v} = 0.\tag{2.6}$$

和牛顿第二定律（2.7）

$$\frac{D\mathbf{v}}{Dt} = \mathbf{g} - \frac{1}{\rho}\text{grad}p + \frac{1}{\rho}\mathbf{f}(\mathbf{v}),\tag{2.7}$$

$$\rho\frac{DU}{Dt} + p\,\text{div}\mathbf{v} = \text{div}(k_c\,\text{grad}\,T) + \Phi_v + \rho Q,\tag{2.10}$$

其中$U$是单位质量的热能，$T$是温度，$k_c$是热传导系数，$\Phi_v$是（每单位体积和单位时间）由粘性摩擦产生的热量，$Q$是（每单位质量）由内部热源产生的净热量。对于本书中要讨论的所有情况，耗散函数$\Phi_v$都可以忽略不计。由于函数$Q$对恒星内部特别相关，它将在3.2节中进一步讨论。

方程解释

这里的单位是 单位体积单位时间内 进出的热能

关于物质微元考虑热能守恒

单位质量的某个值（x/质量）乘以密度（质量/体积）就变成单位体积的某个值（x/体积）

• 左边第一项是单位质量含有的内能变化率
  • 左边的减少它
  • 右边的增加它
• 左边第二项是压力向外做功的速率（功率）
  • 速度散度表示三个方向向外的(距离/时间)之和，压力乘以距离就是做功
• 右边第一项是热传导引起的能量变化率
  • 物质微元作为温度梯度的源，表示外面温度比内部高，那么就有温度增加的趋势
• 右边第二项是粘性耗散产热（在这里被忽略）
• 右边第三项是内部热源

现在，假设流体的每一点都发生准静态变化，我们可以写

$$T\frac{DS}{Dt} = \frac{DU}{Dt} + p\frac{D}{Dt}\left(\frac{1}{\rho}\right),\tag{2.11}$$

其中$S$是单位质量的熵。

方程推导

热力学中的熵只有其变化率的定义，对于可逆过程，有

$$dS = \frac{\delta Q}{T}$$

（不可逆过程要换大于等于号）

其中 $dS$ 是熵增加的速率， $\delta Q$ 是吸收热量的速率， $T$ 是绝对温度

它是相对于封闭系统（固定质量）的，熵仅在与外界产生能量交换时变化，而温度决定了能量交换时熵的变化率

热力学第一定律

$$\delta Q = dU + pdV$$

这里 $dU$ 是内能的变化，$pdV$ 是系统对外做功

代入得到

$$TdS = dU + pdV$$

替换成物质导数

$$T\frac{DS}{Dt} = \frac{DU}{Dt} + p\frac{DV}{Dt}$$

$\frac{1}{\rho}$ 表示单位质量的体积，用这个替换 $V$ 表达更明确的含义

$$T\frac{DS}{Dt} = \frac{DU}{Dt} + p\frac{D}{Dt}\left(\frac{1}{\rho}\right)$$

根据方程(2.6)，比较方程(2.10)和(2.11)得到结果

$$\rho T\frac{DS}{Dt} = \text{div}(k_c\,\text{grad}\,T) + \Phi_v + \rho Q,\tag{2.12}$$

表示当我们沿着质量元素的运动路径时比熵的变化。

方程推导

等式右边没变，实际上就是证明

$$\rho\frac{DU}{Dt} + p \text{div}\mathbf{v} = \rho T\frac{DS}{Dt}$$

把这个代入

$$T\frac{DS}{Dt} = \frac{DU}{Dt} + p\frac{D}{Dt}\left(\frac{1}{\rho}\right),\tag{2.11}$$

得到

$$\rho\frac{DU}{Dt} + p \text{div}\mathbf{v} = \rho \frac{DU}{Dt} + \rho p\frac{D}{Dt}\left(\frac{1}{\rho}\right)$$

只需证明

$$\text{div}\mathbf{v} = \rho \frac{D}{Dt}\left(\frac{1}{\rho}\right)$$

由于

$$D\frac{1}{\rho} = -\frac{1}{\rho^2}D\rho$$

代入就能得到这个形式

$$\frac{1}{\rho} \frac{D\rho}{Dt} + \text{div}\mathbf{v} = 0.\tag{2.6}$$

所以得证

还有个思路

对于

$$\text{div}\mathbf{v} = \rho \frac{D}{Dt}\left(\frac{1}{\rho}\right)$$

首先注意到右边表示密度乘以单位质量体积的物质导数

密度定义是 单位体积的质量

$\frac{1}{\rho}$ 是单位质量的体积

因此单位体积的质量 乘以 单位质量体积的变化率

得到 单位体积的体积的变化率

$$\rho \frac{D}{Dt}\left(\frac{1}{\rho}\right) = \frac{DV}{VDt} = \text{div}\mathbf{v}$$

这就是单位体积向外的通量，是速度散度的定义

要完成方程组，还需要进一步的热力学关系。例如，对于理想气体，我们有

$$U = c_VT\tag{2.13}$$

且

$$p = \frac{\mathcal{R} }{\bar{\mu} } \rho T, \tag{2.14}$$

其中$\bar{\mu}$是平均分子量。我们还有$\mathcal{R}/\bar{\mu} = c_p - c_V$，其中$c_p$和$c_V$分别是恒压比热容和恒容比热容。将这些关系代入方程(2.11)，我们得到

$$S = c_p \log \Theta + constant. \tag{2.15}$$

量

$$\Theta = T \left(\frac{p_0}{p}\right)^{(\gamma-1)/\gamma}, \tag{2.16}$$

其中$p_0$是一个常数参考压力，$\gamma$是绝热指数，被称为势温。对于等熵运动（即方程[2.12]右侧恒等于零的运动），每个流体粒子的势温沿其路径保持恒定。

2.2.2 边界条件

为了求解控制流体运动的偏微分方程，必须规定覆盖所有空间的初始条件和覆盖所有时间的边界条件。虽然初始条件总是特定于手头的问题，但适当的边界条件具有相当普遍的性质。

在固定的固体边界上，不能有穿过边界的流体运动。这个条件意味着

$$\mathbf{n} \cdot \mathbf{v} = 0, \tag{2.17}$$

其中$\mathbf{n}$是表面的外法线。第二个条件由无滑移条件提供，即刚性壁和与之相邻的粘性流体之间不应有相对切向速度。因此，我们还必须规定

$$\mathbf{n} \times \mathbf{v} = \mathbf{0}, \tag{2.18}$$

在固定的固体壁上。

在界面边界（如海洋表面或恒星的外表面），必须规定没有质量元素穿过这个边界，以便边界上的流体粒子保持在边界上。因此，如果$\xi(\mathbf{r}, t)$定义了相对于平衡水平的表面高程，则速度的运动学边界条件为

$$\frac{D\xi}{Dt} = \mathbf{n} \cdot \mathbf{v} \tag{2.19}$$

在物质边界上。如果这个边界是固定的（即$\xi \equiv 0$），条件(2.19)简化为

$$\mathbf{n} \cdot \mathbf{v} = 0, \tag{2.20}$$

表示物质总是沿着规定的物质边界流动。

除了这个运动学边界条件，显然我们还必须确保在任何非固体边界上的力平衡。例如，在恒星的自由表面上重力加速度必须是连续的。同样，作用于非固体边界上的应力矢量的分量必须在该边界上连续（参见方程[2.8]）。因此，我们有

$$[n_k(-p\delta_{ik} + t_{ik})] = 0,\tag{2.21}$$

其中方括号表示该量在非固体边界上的跳跃（$i = 1, 2, 3$）。特别是，在嵌入真空中的恒星模型的自由表面上，这三个分量必须恒等于零。

2.2.3 旋转参考系

在某些应用中，描述运动以相对于以恒定角速度$\Omega$旋转的参考系中静止的观察者所看到的方式是很方便的。我们可以写作

$$\mathbf{v}(\mathbf{r}, t) = \mathbf{u}(\mathbf{r}, t) + \mathbf{\Omega} \times \mathbf{r},\tag{2.22}$$

其中速度$\mathbf{u}$指的是相对于运动轴的速度。同样，物质加速度(2.4)具有如下形式

$$\mathbf{a}(\mathbf{r}, t) = \frac{D\mathbf{u}}{Dt} + 2\mathbf{\Omega} \times \mathbf{u} + \mathbf{\Omega} \times (\mathbf{\Omega} \times \mathbf{r}),\tag{2.23}$$

其中

$$\frac{D\mathbf{u}}{Dt} = \frac{\partial\mathbf{u}}{\partial t} + (\mathbf{u} \cdot \mathrm{grad})\mathbf{u}\tag{2.24}$$

是相对于旋转参考系的加速度。量$2\mathbf{\Omega} \times \mathbf{u}$和$\mathbf{\Omega} \times (\mathbf{\Omega} \times \mathbf{r})$分别表示科里奥利加速度和离心加速度。由于张量(2.8)对于均匀旋转是不变的，方程(2.7)则变为

$$\frac{D\mathbf{u}}{Dt} + 2\mathbf{\Omega} \times \mathbf{u} = \mathbf{g} - \mathbf{\Omega} \times (\mathbf{\Omega} \times \mathbf{r}) - \frac{1}{\rho} \mathrm{grad}\, p + \frac{1}{\rho} \mathbf{f}(\mathbf{u}). \tag{2.25}$$

容易证明

$$\mathbf{\Omega} \times (\mathbf{\Omega} \times \mathbf{r}) = -\mathrm{grad} \left(\frac{1}{2}|\mathbf{\Omega} \times \mathbf{r}|^2\right). \tag{2.26}$$

因为矢量$\mathbf{g}$也可以从标量势$V$（比如说）导出，我们可以将动量方程(2.25)改写为

$$\frac{D\mathbf{u}}{Dt} + 2\mathbf{\Omega} \times \mathbf{u} = \mathbf{g}_e - \frac{1}{\rho} \mathrm{grad}\, p + \frac{1}{\rho} \mathbf{f}(\mathbf{u}), \tag{2.27}$$

其中

$$\mathbf{g}_e = -\mathrm{grad} \left(V - \frac{1}{2}|\mathbf{\Omega} \times \mathbf{r}|^2\right) \tag{2.28}$$

是有效重力。比较方程(2.27)和方程(2.7)，可以很容易看出，科里奥利加速度是相对于旋转参考系的牛顿第二运动定律的唯一结构变化。

早在1835年，法国工程师Gaspard Coriolis (1792-1843)就对旋转参考系中运动物体的绝对加速度进行了详细的数学研究。他的工作对当时的气象学研究几乎没有产生影响，以至于在整个十九世纪期间，我们对旋转流体行为的认知几乎没有取得进展。事实上，直到19世纪50年代末，美国气象学家威廉·费雷尔（William Ferrel，1817-1891年）才首次对旋转地球上的大气运动进行了数学公式化。此外，正如我们将在2.6.1节中看到的，地球自转对风驱动海洋洋流的偏转力的重要性直到二十世纪初才被认识到。例如，英国学者亚瑟·埃丁顿（Arthur Eddington，1882-1944年）在1925年注意到，恒星辐射区域中的大尺度子午线环流会因恒星的自转而向东西方向偏转，但直到1941年冈纳·雷塞兰（Gunnar Randers，1914-1992年）才对旋转恒星中粘性力和偏转力之间的平衡进行了首次详细分析（参见公式[4.49]）。

对于稳定流动，在旋转坐标系中测量的加速度和科里奥利加速度的相对重要性可以估计为

$$\frac{|\mathbf{u} \cdot \mathrm{grad}\, \mathbf{u}|}{|\Omega \times \mathbf{u}|} \approx \frac{U^2/L}{\Omega U} = \frac{U}{\Omega L}, \tag{2.29}$$

其中$U$和$L$分别是流动的特征速度和长度。这个比值是一个无量纲数，称为罗斯比数，用$Ro$表示：

$$Ro = \frac{U}{\Omega L}. \tag{2.30}$$

类似地，利用方程(2.9)，可以很容易地估算粘性力与科里奥利力的比值。得到：

$$\frac{|\nu\nabla^2\mathbf{u}|}{|\Omega \times \mathbf{u}|} \approx \frac{\nu U/L^2}{\Omega U} = \frac{\nu}{\Omega L^2}, \tag{2.31}$$

其中$\nu = \mu/\rho$是运动粘度系数。无量纲数

$$E = \frac{\nu}{\Omega L^2} \tag{2.32}$$

被称为埃克曼数。